数学建模(二)---多目标优化
2024-04-07线性规划具有一定的局限性,其只能解决一组线性约束条件下,某一目标只能是一个目标的最大或最小值的问题。但是在实际决策中,衡量方案优劣需要考虑多个目标,这些目标中,有主要的,也有次要的;有最大值的,也有最小值的;有定量的,也有定性的;有相互补充的,也有相互对立的。目标规划(Goal Programming)是美国经济学家查恩斯(A. Charnes)和库柏(W. W. Cooper)在 1961年出版的《管理模型及线性规划的工业应用》一书中,首先提出的。
①所有目标函数统一成max形式(或统一成min形式);
②总目标为一个加权求和形;
①先保证主要目标,再考虑次要目标;
②有绝对约束和目标约束;
决策者根据实际情况为每个子目标指定权重w1,w2,.....,wk,其中,wi/wj为第i个目标关于第j个目标的相对重要性。那么根据目标形式,得出对应的总目标为:
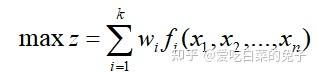
于是我们就可以把多目标优化转化为一般的单目标模型:
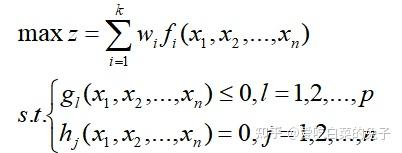
例题:某厂计划在下一个生产周期内生产A,B两种产品,每种产品的单位利润分别为10和18(单位:万元),资源消耗和限制数量如下表,求总利润最大的生产方案。
| A | B | 限制 | |
| 原料1/单位产品 | 5 | 2 | 170 |
| 原料2/单位产品 | 2 | 3 | 100 |
| 人工/单位产品 | 1 | 5 | 150 |
解:设A,B,C分别为x1,x2,x3个单位,数学模型为:

这是一个单目标问题,解得x1=50/7,x2=200/7,最优目标函数值z=4100/7万元。
但是如果考虑到第一种资源面临涨价预期,希望尽可能清空库存利于快速补充,故考虑本期利润最大化的同时必须为下一个周期做好准备,从而增加新目标函数:

进而就被转化为了一个多目标问题。
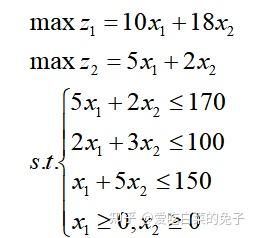
如果目标一比目标二更重要,根据需求设定目标一相比目标二的重要性是2:1,则2个目标可以统一为:

这样,多目标问题就被化为常规的单目标线性规问题了。

解得x1=550/23,x2=580/23,最优解为:z=1556.087。
下面引入与建立不同级的多目标规划数学模型有关的概念。
设d为决策变量的函数,正偏差变量(表示决策值超过目标值的部分):
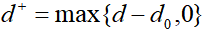
负偏差变量(表示决策值未达到目标值的部分):
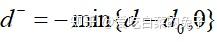
这里d0表示d的目标值。因决策值不可能既超过目标值同时又未达到目标值,即恒有d+*d-=0。
绝对约束是指必须严格满足的等式约束和不等式约束;如线性规划问题的所有约束条件,不能满足这些约束条件的解称为非可行解,所以它们是硬约束。目标约束是目标规划特有的,可把约束右端项看作要追求的目标值。在达到此目标值时允许发生正或负偏差,因此在这些约束中加入正、负偏差变量,它们是软约束。线性规划问题的目标函数,在给定目标值和加入正、负偏差变量后可变换为目标约束。也可根据问题的需要将绝对约束变换为目标约束。
一个规划问题常常有若干目标。但决策者在要求达到这些目标时,是有主次或轻重缓急的不同。凡要求第一位达到的目标赋于优先因子P1,次位的目标赋于优先因子P2,...,并规定pk>>pk+1,k=1,2,....,q,表示pk比pk+1有更大的优先权。以此类推,若要区别具有相同优先因子的两个目标的差别,这时可分别赋于它们不同的权系数wj,这些都由决策者按具体情况而定。
目标规划的目标函数(准则函数)是按各目标约束的正、负偏差变量和赋于相应的优先因子而构造的。当每一目标值确定后,决策者的要求是尽可能缩小偏离目标值。因此目标规划的目标函数只能是:

其基本形式有三种:
1)要求恰好达到目标值,即正、负偏差变量都要尽可能地小,这时
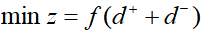
2)要求不超过目标值,即允许达不到目标值,就是正偏差变量要尽可能地小,这时
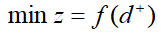
3)要求超过目标值,即超过量不限,但必须是负偏差变量要尽可能地小,这时
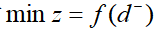
对每一个具体目标规划问题,可根据决策者的要求和赋于各目标的优先因子来构造目标函数,以下用例子说明。
例1 某工厂生产I,Ⅱ两种产品,已知有关数据见表1,决策者在原材料供应受严格限制的基础上考虑:首先是产品 II 的产量不低于产品 I 的产量;其次是充分利用设备有效台时,不加班;再次是利润额不小于56 元。求决策方案。

解:按决策者所要求的,分别赋于这三个目标P1,P2,P3优先因子。这问题的数学模型是:
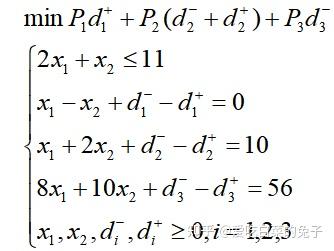
设xj(j=1,2,.....,n)是目标规划的决策变量,共有m个约束是刚性约束,可能是等式约束,也可能是不等式约束。设有l个柔性目标约束,其目标规划约束的偏差为d(+)i,d(-)i(i=1,2,...,l).设有q个优先级别,分别为P1,P2,...,Pq。在同一个优先级Pk中,有不同的权重,分别记为w(+)kj,w(-)kj(j=1,2,...,l)。因此目标规划模型的一般数学表达式为:

建立目标规划的数学模型时,需要确定目标值、优先等级、权系数等,它们都具有一定的主观性和模糊性,可以用专家评定法给以量化。
序贯式算法是求解目标规划的一种早期算法,其核心是根据优先级的先后次序,将目标规划问题分解成一系列的单目标规划问题,然后再依次求解。
求解目标规划的序贯算法:
对于k=1,2,...,q,求解单目标规划:

其最优目标值为z(*)k,当k=1时,第三个约束为空约束。当k=q时,z(*)q所对应的解x(*)为目标规划的最优解。
注:此时最优解的概念与线性规划最优解的概念已有所不同,但为方便起见,仍称为最优解。




