Adam optimizer浅析_首页-多利娱乐-全球注册站

Adam optimizer浅析

2024-04-07

ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION

1.背景

优化问题一直是机器学习的核心问题之一，毕竟不管怎么折腾最后基本都会回到优化函数上来。而优化结果又可能受到多种因素的影响，比如局部最优解陷阱, 收敛速率，鞍点等等。最开始采用的是batch gradient descent，也就是对整个数据集拟合寻求最优解。然而这个方法有好几个问题，其中一个就是如果在一个极大的数据集上求梯度，那么每一次迭代所花的时间都是相当长的，效率太低下。自然与之对应的就是每次只取一个(stochastic gradient descent) 或几个(min-batch gradient descent)，这样可以提高运算效率同时减少收敛至局部最优解的可能性。那么还有没有收敛效率更快的算法呢，这篇文章提供了一个可能的结果，采用adaptive moment estimation(adam)的方法来对高纬度的数据进行快速拟合，adam结合了AdaGrad(用来处理稀疏梯度)以及RMSProp(处理在线数据)的优点，并且不需要设置步长的衰减。

2.算法

2.1 算法演变

在说到adam之前就得先捋一下优化算法的来龙去脉。尽管SGD在很多模型及数据库上都取得了出色的成果，但是有一个问题就是有时收敛速率会很慢。这个问题在现在动辄就要训练好几天的大型数据集上就显得十分重要，那么一个自然而然的想法就是利用动量(momentum)，利用当前位置的梯度结合过去累积的梯度来优化。将其结合进SGD就诞生了最基本的结合动量的优化方法。需要注意的是momentum在这里扮演了阻力的角色，也就是如果梯度的方向来回波动，那么momentum可以减少波动对于整体收敛方向的影响，以此来加快收敛速率。

但是这个算法没有解决两个问题：

1）模型参数的初始设定对收敛的影响

2）由于引入了更多的超参数，那么超参数的设定对收敛的有很大影响

接下来的模型主要还是针对第二点，尤其是学习速率对于收敛的影响。直观上来说，如果梯度一直保持同一个方向，那么可以适当增大学习速率，相反则减少学习速率。Adagrad采用了类似的思想，同说提出可以用累积的动量来rescale梯度从而达到控制学习速率的目的。但这个就有一个很明显的问题，如果前几次梯度方向相同，那么 $r$ 的值就会很快变得很大，结果模型居然就这么收敛了？！实验也证明了这一点。因此这个方法要求初始学习速率一定要很小，而且最好是凸优化问题，毕竟只有一个最优解，RMSProp则优化了这个问题。

RMSProp 采用了exponential moving average的办法，可以理解为一种加权的平均数，在迭代的过程中，越早的梯度对于当前动量的影响就越小,因此整体动量可以维持在一个较为稳定的范围内而不像adamGrad一样有迅速收敛的危险。大量实验也证明在优化非凸函数的任务上，这个方法基本都是最优解。

接下来就是本文推出的adam算法了，接下来会详细介绍。

2.2 update rule

adam的一大特征就是可以较好的选择步长，假设 $\\epsilon=0$ ,那么在第t步时的步长为 $\\Delta_t=\\alpha\\cdot\\hat{m}_t/\\sqrt{\\hat{v}_t}$ ，其上界可以表示为

$|\\Delta_t|\\leq\\alpha\\cdot(1-\\beta_1)/\\sqrt{1-\\beta_2}$ 当 $1-\\beta_1 > \\sqrt{1-\\beta_2}$ ,

$|\\Delta_t|\\leq\\alpha$ 当 $1-\\beta_1 \\leq \\sqrt{1-\\beta_2}$

第一种情况基本只在数据极其稀疏的情况下发生。在大多数情况下，由于 $| \\mathbb{E[g]}| /| \\mathbb{E[g^2]}| \\leq1$ ，可得 $\\left|\\widehat{m}_{t}/ \\sqrt{\\widehat{v}_{t}}\\right|\\approx1$ , 因此 $\\Delta_t$ 的上界可以表示为 $\\alpha$ 。文章在这里将 $\\hat{m}_{t}/ \\sqrt{\\hat{v}_{t}}$ 定义为信噪比，当这个信噪比较小的时候意味着在这个点的不确定性较大，根据经验通常在接近极值点的时候信噪比接近0.这就达到了对学习率退火的目的，同时也使得梯度的scale对于优化没有太大影响。

可以看到与RMSProp的主要区别为不仅对二次动量做平均，同时也对一次动量做平均，并且引入了对于动量误差的修正。

2.3 initialization bias correction

文章对二次moment的估计采用了exponential moving average方法，为了证明其有效性，首先有如下公式：

$v_t=(1-\\beta_2)\\sum\\limits_{i=1}^{t}\\beta_2^{t-i}\\cdot g_i^{2}$

那么为了修正 $\\mathbb{E[v_t]}$ 对于真正的二次moment $\\mathbb{E[g_t^2]}$ 的偏差,有如下公式：

$\\begin{aligned}\\mathbb{E}\\left[v_{t}\\right]&=\\mathbb{E}\\left[\\left(1-\\beta_{2}\\right) \\sum_{i=1}^{t}\\beta_{2}^{t-i}\\cdot g_{i}^{2}\\right]\\\\ &=\\mathbb{E}\\left[g_{t}^{2}\\right]\\cdot\\left(1-\\beta_{2}\\right) \\sum_{i=1}^{t}\\beta_{2}^{t-i}+\\zeta \\\\ &=\\mathbb{E}\\left[g_{t}^{2}\\right]\\cdot\\left(1-\\beta_{2}^{t}\\right)+\\zeta \\end{aligned}$

当 $\\mathbb{E[g_t^2]}$ 不变时， $\\zeta$ 为0，而且在其他情况下只需要使 $\\beta_2 < 1$ 就基本可以保证 $\\zeta$ 的值很小，因此可以将其忽略不计。那么就可以得出：

$\\mathbb{E[g_t^2]}=\\mathbb{E[v_t]/(1-\\beta_2^t)}$

那么也就可以推出 ${\\widehat{v}_{t}\\leftarrow v_{t}/\\left(1-\\beta_{2}^{t}\\right)}$

2.4 convergence analysis

这里的证明过程采用了online learning 的证明方法，假设有一系列未知的凸函数 $f_1(\ heta),f_2(\ heta)...f_T(\ heta)$ ,在时间t需要需要预测参数 $\ heta_t$ 并计算 $f_t(\ heta_t)$ 的值。

首先定一个regret函数， $R(T)=\\sum_{t=1}^{T}\\left[f_{t}\\left(\ heta_{t}\\right)-f_{t}\\left(\ heta^{*}\\right)\\right]$ ，

其中 $\ heta^{*}=\\arg \\min _{\ heta \\in \\mathcal{X}}\\sum_{t=1}^{T}f_{t}(\ heta)$ 。

经过一番推导得出 $\\frac{R(T)}{T}=O\\left(\\frac{1}{\\sqrt{T}}\\right)$ ,

由此可得 $\\lim _{T \\rightarrow \\infty}\\frac{R(T)}{T}=0$ ，收敛性也由此证明。

2.5 adammax

在adam中 $v_t$ 可以理解为 $L^2$ norm,可以进一步将其泛化为 $L^p$ norm. 当 $p\\rightarrow \\infty$ 时，假设

$u_t=\\lim\\limits_{p\\rightarrow \\infty}(v_t)^{1/p}$ ,由于

$\\begin{aligned}v_{t}&=\\beta_{2}^{p}v_{t-1}+\\left(1-\\beta_{2}^{p}\\right)\\left|g_{t}\\right|^{p}\\\\ &=\\left(1-\\beta_{2}^{p}\\right) \\sum_{i=1}^{t}\\beta_{2}^{p(t-i)}\\cdot\\left|g_{i}\\right|^{p}\\end{aligned}$

经过一些列推导可得： $u_t=max(\\beta_2 \\cdot u_{t-1},|g_t|)$ .

算法如下

2.6 temporal averaging

由于在接近最优解时噪音比较大，作者在这列采用了和之前类似的做法，

$\\bar{\ heta}_{t}\\leftarrow \\beta_{2}\\cdot \\bar{\ heta}_{t-1}+\\left(1-\\beta_{2}\\right) \ heta_{t}$

并对 $\\bar{\ heta}_{t}$ 进行bias term correction使得 $\\widehat{\ heta}_{t}=\\bar{\ heta}_{t}/ (1-\\beta_2^t)$ ，推导同2.3。

3 实验

文章在多种机器学习算法上测试了adam optimizer的效果。

3.1 logestic regression

逻辑回归是标准的凸函数，因此在优化时不需要担心局部最优解的问题.第一个对比是在MNIST上，计算时采用 $\\alpha_t=\\frac{\\alpha}{\\sqrt{t}}$ 的衰减，可以看到adam在收敛速率上于sgd+nesterov momentum 接近，快于adaGrad.第二个则是在IMDB movie review 上，由于数据较为稀疏，可以看到SGD的表现并不好，相对的adam 于adagrad都强于SGD.

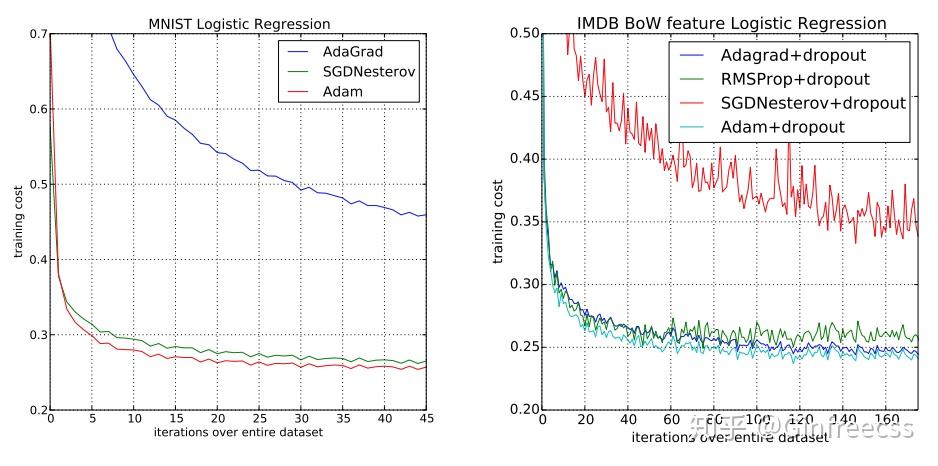
3.2 MULTI-LAYER NEURAL NETWORKS

第二个结构就是常用的多层神经网络，由于通常用来拟合非凸函数，因此可以测试optimizer不受局部最优解限制的能力。可以看到adam在收敛速率以及最小化损失函数上都比其他optimizer出色。

3.3 CONVOLUTIONAL NEURAL NETWORKS

接下来的测试就是更复杂化的feed-forward network，卷积神经网络，用来测试adam是否能针对不同的module都取得不错的优化结果。这次是在传统的CIFAR10上，adam仍然取得了最好的结果。

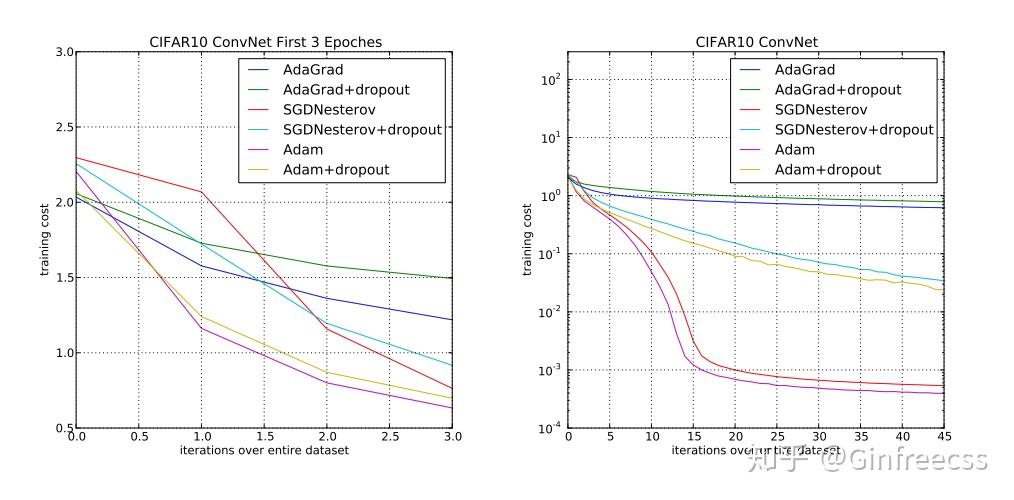
3.4BIAS-CORRECTION TERM

这部分测试了一下对于variational auto encoder，bias-correction term 对于结果的影响，其中绿线为移除bias term的结果，红线为保留bias term的结果。由于移除bias term之后，adam的算法比较接近于RMSProp，因此可以得出adam的优化能力不弱于RMSProp。

4 结论

自从adam推出之后可以说是收到了万千宠爱，大部分的学习模型都开始采用adam作为优化方案。但是adam并不代表着可以应用在所有情况下。比如on the convergence of adam and beyond，这篇提供了一个反例来说明Adam有可能不收敛，并提供了一个新的算法AMSGRAD。大意是由于adam采用了一个滑窗内的累积，因此 $v_t$ 的变化并不单调，并不能保证学习率会在最后收敛，并对其二阶动量进行了修改，

$v_t=max(\\beta_2 * v_{t-1}+ (1-\\beta_2) g_t^2, v_{t-1})$

采用这个方法保证了 $v_t$ 的单调性，从而使得学习率递减。

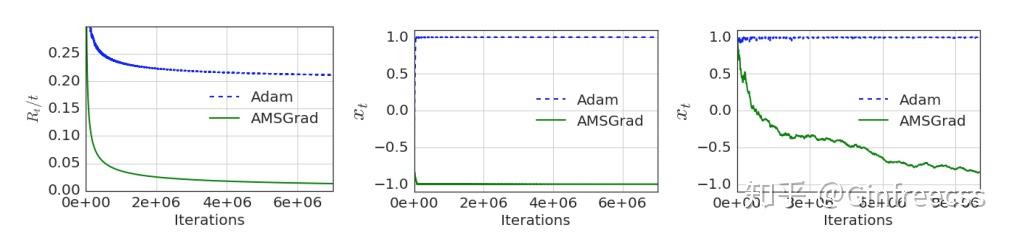
可以看到在这种情况下adam完全没有收敛，不过感觉这是一种比较极端的情况并不算太常见。

还有一篇就是adam 虽然收敛快但是找到的最优解未必比SGD, 在 Improving Generalization Performance by Switching from Adam to SGD 这篇文章中，提出可以先用adam然后在训练的后半段转换成SGD训练。不过据说转换条件比较苛刻。
总之合适的优化方法还是根据所要解决的问题以及数据来决定，并没有一个固定的最佳解法，多调参才是正经的。

5 reference

[1]Diederik P.Kingma, Jimmy Lei Ba, Adam: A method for Stochastic Optimizaiton, ICLR 2015

[2]on the convergence of adam and beyond, Sashank J. Reddi, Satyen Kale & Sanjiv Kumar ICLR2018.

[3]Improving Generalization Performance by Switching from Adam to SGD, Nitish Shirish Keskar,Richard Socher, 2017

上一篇：中央国家机关住房资金管理中心：加大北京市行政区域内租房消费支持力度

下一篇：智能优化算法：蝗虫优化算法-附代码